微积分是高等代数的入门基础,必须掌握的知识。要理解微积分,必须先了解为什么需要微积分,这样才能更好的的掌握。

微积分发展,一般认为经历了三个阶段,第一个阶段是极限概念,这个概念其实很早以前就被提出了,比如说中国古代的庄子、古希腊的阿基米德等均提出过极限的概念。第二个阶段是求积的无限小阶段,这个阶段也在很久前被提出,如我国著名的数学文献《九章算术》就提出圆形分割求面积法。第三个阶段则是微积分互逆关系,最后一个阶段是由牛顿、莱布尼兹完成的。如果说前面两个阶段是萌芽阶段,那么在第三阶段就是发展成熟阶段,最终发展出现代高等代数的基础——微积分学。

微分的几何意义,如函数y=f(x)的图形是一条曲线,并且函数是可微的,曲线上一点M的坐标是[x0,y0],那么如果P发生了一点变化,变成了N点,也就是横坐标增量为△x时,对应纵坐标的增量为△y。
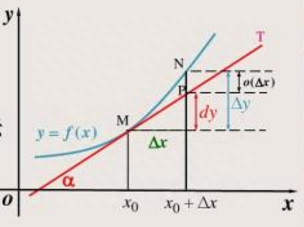
通过M点做一条切线T,曲线上N点在T线上对应的点为P点,P点的横坐标也为x0+△x,纵坐标为y0+dy,也就是说,相对M点而言,T线上发生增量△x对应纵坐标的增量为dy。如果△x很小,小到MN段曲线可以认为是一条直线,一条经过M点的且和切线T重合的直线,那么这时候就可以认为△y无限接近于dy。
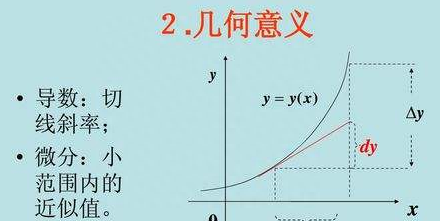
这下就好办了,如果曲线上任何一点都可以变化为切线来求,也就是说微分是一个“以直代曲”的思想,那么问题就变得很简单了,这便是微分的几何意义。
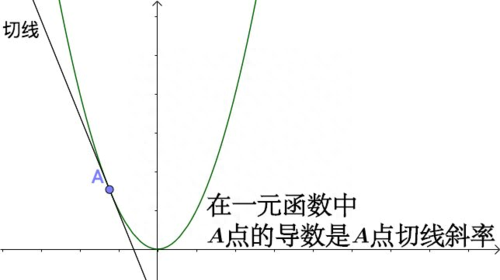
导数的几何意义是切线斜率,对于物理研究而言应该是变化率,然而说法还是不够准确,准确的说法应该是导数是寻找线性近似的概念。上面说了微分是“以直代曲”的概念处理问题,而这个“直”则来自于导数寻找出来的的“线性近似”。在微分中,曲线横坐标(自变量)的“变化量”引起纵坐标(因变量)的“变化量”,在极限概念中,近似等同于该点的线性直线的“变化量”。也就是说,微分的本质就是将复杂问题用极限的分割方法,分割至可以用简单问题的解决方法去解决。

圆分割为无限个圆环,圆环≈矩形
我们知道斜率k的计算是纵坐标之间距离除以横坐标之间距离,也就是y=kx+b,如果这条斜线穿过原点时,就可以表达为y=kx。如果f'(x)为切线斜率,那么根据切线公式可由斜率和横轴增量的乘积f'(x)△x求得纵轴的增量,即dy,导数的表达式为f'(x)=dy/dx,也称为微商(可不是现在网络上流行的卖东西的“微商”)。
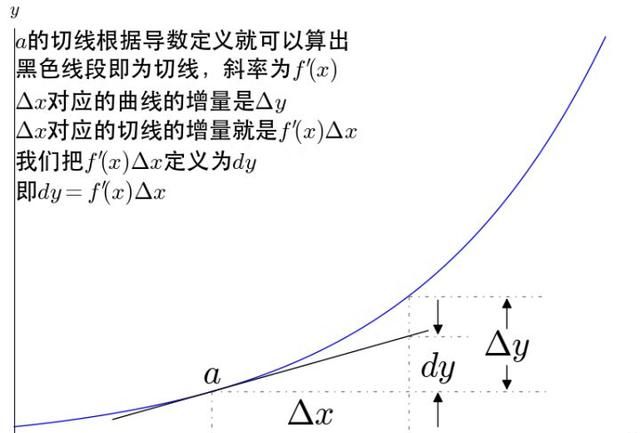
在可导函数y=f(x)中,如果自变量x的微分dx定义为自变量x的改变量△x,那么函数在任意一点上的微分都可以表达为dy=f'(x)dx。
所以,导数和微分的区别在于,导数是一个变化率,如斜率,而微分则是一个线性段,其由斜率(导数)和自变量增量(变量)乘积而来的切线上的线性直线段(近似)。
最后举一个例子:小明骑自行车,出发时间为0点,每个时间点用x来表示,如可以表示为2.2222(转为十进制)点钟,y是小明从0点到x点所走的路程,那么:dx则为一个极小的时间分割段(近乎一个点),如2.2222……,dy则为dx时间内所走的路程,而y'(x)=dy/dx则是小明的速度变化率(速度函数,在dx时间内,可以近似认为该段时间内速度是匀速的)。
要真正的了解这个世界,了解这个世界的东西,微积分是一个必要的工具,一个可以将复杂的变化规律归纳至数学的形式——一种人类智慧所特有的理解能力的工具,至少不是不能言传只能意会那种玄意吧。